Geometry is the branch of mathematics which includes the study of shapes, size and relative position of figures. Geometry has two parts namely, Plane geometry, Solid geometry.
Plane geometry: It deals with two-dimensional or 2D objects like line, circle, triangle etc. These shapes can be easily drawn on paper. 2D shapes have only two dimensions namely length and breadth.

Solid geometry: It deals with three-dimensional or 3 D objects with some depth like cube, sphere, cuboid, prism etc. These shapes are a bit complicated to be drawn on paper. 3D shapes have three dimensions namely length, breadth and depth.
We must understand the following basic terms before getting into actual geometry. These terms refer to the basic objects which make up the geometric shapes.
Point: The following are the properties of a point,
- It is a location in space.
- A point does not have a length or width or any thickness.
- It is generally represented by a dot.
- Points are usually named with capital letter.
For example, in the picture shown we are representing the dots as "point A, point B and point C".

Line: The following are the properties of a line,
- A line is a group of points.
- A line has length but no breadth.
- The points in a line may extend infinitely.
- It is generally represented by a line with two arrows over the letters depicting the points.
- The two arrows are used to show that the line extends infinitely.
For example, in the picture shown we are representing the line as ‘XY’. We can also call it line ‘YX’.

Some useful information about lines
- For a given point, there are infinite numbers of lines passing through it. These lines are called as concurrent lines.
- There is one and only one line passing through two distinct points.
- The intersection of two distinct lines is a point.
- Three or more points are said to be collinear if they lie on a line.
- Three or more points are said to be non-collinear if they do not line on a line.
- There are an infinite number of planes passing through any given line.
- There is exactly one plane passing through three non-collinear points.
- Two distinct intersecting lines lie in a plane.
- Two or more lines are said to be coplanar if they lie in same plane.
- Two or more lines are said to be non-coplanar if they do not lie in same plane.
- If two or more points lie in a plane, the whole line lies in the plane
- A-X-B implies that the points “A, X, B” are collinear and that point X lies between A and B.
- The intersection of two planes is a line
- A line which intersects two or more given coplanar lines in distinct points is called a transversal of the given lines.
- A line which is perpendicular to a line segment and passes through the midpoint of the segment is called the perpendicular bisector of the segment.
- Every point on the perpendicular bisector of a segment is equidistant from the two endpoints of the segment.
Line segment: The following are the properties of a line segment,
- A line segment is part of a line.
- It has two endpoints with the capital letters depicting the points.
- A line segment has length but no breadth.
- A line has no endpoints whereas the line segment has end points.
- It is generally represented by a line over the letters depicting the points
For example, in the picture shown we are representing line segment as ‘XY’.

Difference between Line and Line segment
| Line |
Line segment |
| A line is a group of points. |
A line segment is part of a line. |
| A line has no endpoints. |
A line segment has end points. |
| The points in a line may extend infinitely. |
The points in a line are defined. |
| It is represented by a line with two arrows over the letters depicting the points. |
It is represented by a simple line over the letters depicting the points. |
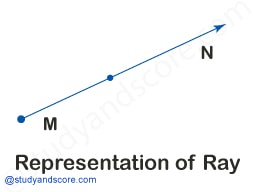
Ray: The following are the properties of a ray,
- A ray is a collection of points which start at one point and extend infinitely in one direction.
- A ray has length but no breadth.
- It has an endpoint and an arrow depicted with capital letters.
For example, in the picture shown we are representing the ray as ‘MN’.
Angle: Two rays having a common or same endpoint forms as angle.
- The corner point of an angle is called the vertex.
- The two straight sides are called arms. The angle is the extent of turn between each arm.
For example, in the picture shown we are representing an angle A. Two rays AB and AC have a common endpoint A.

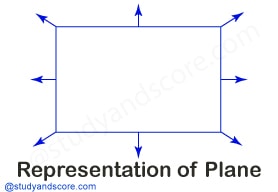
Plane: It is a level, even and flat surface just like a piece of paper.
- It extends forever and ever in all directions.
- It has infinite width and length.
- We can use arrows to show that it extends in all directions forever.
- Share with your friends! -







Login to post your comment here...
- or with social Account -